GemPy: 3D Structural Geomodeling in Python
Contents
GemPy: 3D Structural Geomodeling in Python¶
Making 3D geological models is hard. Classical explicit models rely on the expertise of the modeller and their manufactured nature makes them extremely tedious to update as more information is obtained. Implicit modelling based on global interpolations can solve many of these problems, but so far they have been implemented in commercial software only, making them often prohibitively expensive for scientists. Also, proprietary geomodeling software tends to only provide limited functionality through their interfaces or APIs, limiting modern reproducible geocomputing workflows.
Making a 3D geomodel is hard, but making 50 different models for testing different hypotheses or 50000 models to get a complete description of the inherent model uncertainty is much harder. And it was in this climate of frustration and limitation—as is the case with many other open-source projects—when GemPy was conceived.
GemPy is an open-source Python library based on the potential field method developed by Lajaunie et al. [LCM97] and expanded during the following years by many others. The method interpolates interface points and surface poles—i.e perpendicular vectors to the surface dip—to create a potential field from which the domains (e.g. layers) can be extracted Figure 7. And by conditioning this potential field and combining multiple of them, it is possible to model faults and unconformities.
Example¶
To create a GemPy model, we have to define its extent, the grid resolution to be used for discretization, as well as the input surface points and orientations, as well as the geological relations of the data.
import gempy as gp
geomodel = gp.create_model("Geomodel Name")
gp.init_data(geomodel, extent, resolution, surfacepoints, orientations)
geological_information = {
"Fault Series": 'Main Fault',
"Stratigraphy Series": ('Sandstone 2', 'Siltstone', 'Shale', 'Sandstone 1')
} gp.map_stack_to_surfaces(geomodel, geological_information) gp.set_interpolator(geomodel)
Then, we can compute the geomodel using:
gp.map_stack_to_surfaces(geomodel, geological_information) gp.set_interpolator(geomodel)
and visualize the geomodel using GemPy’s 2D and 3D visualization functionality:
gp.plot.plot_2d(geomodel)
gp.plot.plot_3d(geomodel)

Fig. 7 Figure caption needed¶
As most other open-source projects, GemPy rests on the shoulders of powerful open-source libraries: pandas [McK10] for data management, pyvista [SK19] for 3-D visualization and scikit-image [WSchonbergerNI+14] for extracting 3D surfaces from the interpolated potential fields, to just name a few. Thus GemPy is another example of how much can be accomplished by integrating the latest developments of the scientific community in the open-source software scene.
One of the main motivations for the development of GemPy was to enable the seamless interoperability with other open-source software to enable uncertainty quantification of geomodels. Every object of GemPy is accessible and easy to modify, thus making stochastic simulations of any aspect of a geomodel straight-forward.
stochasticmodel = StochasticModel(geomodel)
for i in range(1000):
sample_data = stochasticmodel.sample()
stochasticmodel.modify(*sample_data)
gp.compute_model(geomodel)
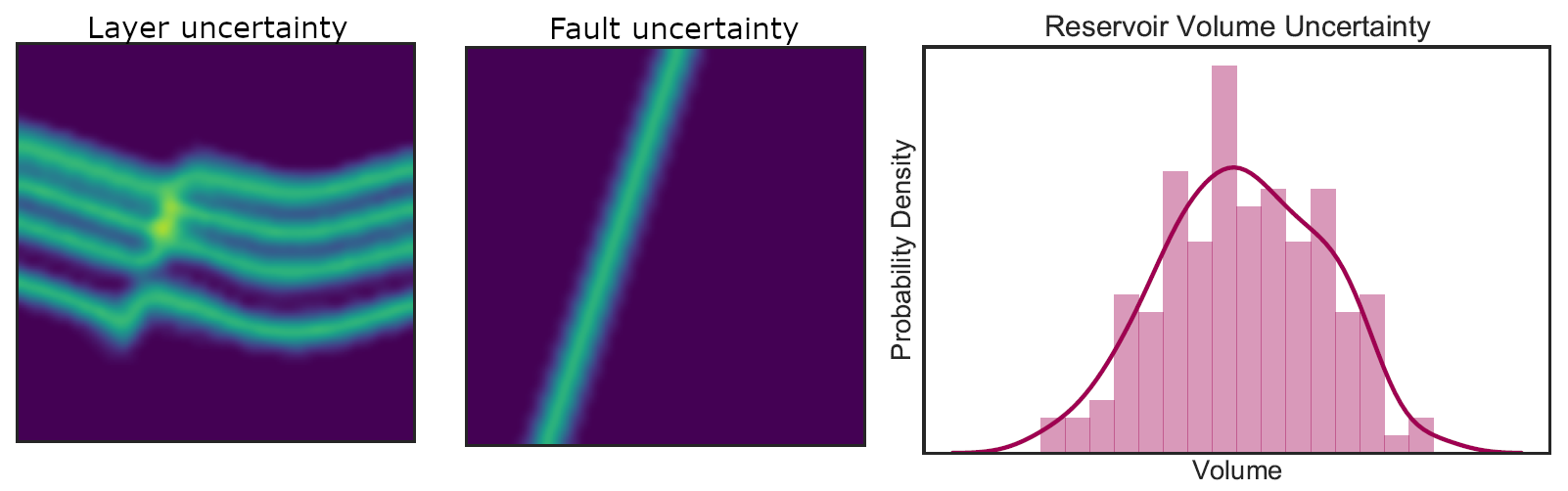
Fig. 8 Figure Caption needed¶
For stochastic simulations, computational performance is key. For this, GemPy was built using theano [TheTDTeamARA+16], and will soon be ported to tensorflow. Both libraries allow us to compute the geomodels on the GPU, significantly decreasing computational time. Our initial research purpose for GemPy was to learn uncertain geological models on additional information (e.g. gravity data, knowledge of the regional geology) using probabilistic machine learning (Bayesian networks). This is greatly helped by its seamless integration into pymc3 [SWF16], a probabilistic programming framework, allowing us to use gradient-based sampling methods to explore the Bayesian posterior model space efficiently.
But this is only the beginning. Making geological modelling open-source is another step towards an ecosystem were geological modelling, geophysical inversions and process simulations coexist, moving from deterministic unique models to an automatic stochastic system of validation of hypothesis - and where the reproducibility of structural geomodelling is not locked behind prohibitive paywalls.
References¶
- LCM97
Christian Lajaunie, Gabriel Courrioux, and Laurent Manuel. Foliation fields and 3d cartography in geology: principles of a method based on potential interpolation. Mathematical Geology, 29(4):571–584, 5 1997. [Online; accessed 2022-01-18]. URL: http://link.springer.com/10.1007/BF02775087, doi:10.1007/BF02775087.
- McK10
missing booktitle in mckinney_data_2010
- SWF16
John Salvatier, Thomas V. Wiecki, and Christopher Fonnesbeck. Probabilistic programming in Python using PyMC3. PeerJ Computer Science, 2:e55, 4 2016. [Online; accessed 2022-01-18]. URL: https://peerj.com/articles/cs-55, doi:10.7717/peerj-cs.55.
- SK19
C. Sullivan and Alexander Kaszynski. Pyvista: 3d plotting and mesh analysis through a streamlined interface for the Visualization Toolkit (VTK). Journal of Open Source Software, 4(37):1450, 5 2019. [Online; accessed 2022-01-18]. URL: http://joss.theoj.org/papers/10.21105/joss.01450, doi:10.21105/joss.01450.
- WSchonbergerNI+14
Stéfan Walt, Johannes L. Schönberger, Juan Nunez-Iglesias, François Boulogne, Joshua D. Warner, Neil Yager, Emmanuelle Gouillart, and Tony Yu. Scikit-image: image processing in Python. PeerJ, 2:e453, 6 2014. [Online; accessed 2022-01-18]. URL: https://peerj.com/articles/453, doi:10.7717/peerj.453.
- TheTDTeamARA+16
The Theano Development Team, Rami Al-Rfou, Guillaume Alain, Amjad Almahairi, Christof Angermueller, Dzmitry Bahdanau, Nicolas Ballas, Frédéric Bastien, Justin Bayer, Anatoly Belikov, Alexander Belopolsky, Yoshua Bengio, Arnaud Bergeron, James Bergstra, Valentin Bisson, Josh Bleecher Snyder, Nicolas Bouchard, Nicolas Boulanger-Lewandowski, Xavier Bouthillier, Alexandre Brébisson, Olivier Breuleux, Pierre-Luc Carrier, Kyunghyun Cho, Jan Chorowski, Paul Christiano, Tim Cooijmans, Marc-Alexandre Côté, Myriam Côté, Aaron Courville, Yann N. Dauphin, Olivier Delalleau, Julien Demouth, Guillaume Desjardins, Sander Dieleman, Laurent Dinh, Mélanie Ducoffe, Vincent Dumoulin, Samira Ebrahimi Kahou, Dumitru Erhan, Ziye Fan, Orhan Firat, Mathieu Germain, Xavier Glorot, Ian Goodfellow, Matt Graham, Caglar Gulcehre, Philippe Hamel, Iban Harlouchet, Jean-Philippe Heng, Balázs Hidasi, Sina Honari, Arjun Jain, Sébastien Jean, Kai Jia, Mikhail Korobov, Vivek Kulkarni, Alex Lamb, Pascal Lamblin, Eric Larsen, César Laurent, Sean Lee, Simon Lefrancois, Simon Lemieux, Nicholas Léonard, Zhouhan Lin, Jesse A. Livezey, Cory Lorenz, Jeremiah Lowin, Qianli Ma, Pierre-Antoine Manzagol, Olivier Mastropietro, Robert T. McGibbon, Roland Memisevic, Bart Merriënboer, Vincent Michalski, Mehdi Mirza, Alberto Orlandi, Christopher Pal, Razvan Pascanu, Mohammad Pezeshki, Colin Raffel, Daniel Renshaw, Matthew Rocklin, Adriana Romero, Markus Roth, Peter Sadowski, John Salvatier, François Savard, Jan Schlüter, John Schulman, Gabriel Schwartz, Iulian Vlad Serban, Dmitriy Serdyuk, Samira Shabanian, Étienne Simon, Sigurd Spieckermann, S. Ramana Subramanyam, Jakub Sygnowski, Jérémie Tanguay, Gijs Tulder, Joseph Turian, Sebastian Urban, Pascal Vincent, Francesco Visin, Harm Vries, David Warde-Farley, Dustin J. Webb, Matthew Willson, Kelvin Xu, Lijun Xue, Li Yao, Saizheng Zhang, and Ying Zhang. Theano: a Python framework for fast computation of mathematical expressions. arXiv:1605.02688 [cs], 5 2016. arXiv: 1605.02688. URL: http://arxiv.org/abs/1605.02688.
